DCF 估值方法¶

DCF是一种估值方法，主要用于评估企业或项目的未来现金流的现值。现值可以用来指导当前的价格与未来预期收益之间的关系，进而指导投资。

DCF的公式很简单，如果你已经理解了它，如下：

\[ \begin{align*} & DCF = \sum_{t=1}^\infty \frac{CF_t}{(1 + r)^t} &(1) \\\ & DCF = \sum_{t=1}^{n} \frac{CF_t}{(1 + r)^t} + \frac{TV}{(1 + r)^n} &(2) \\\ & TV = \frac{CF_{n+1}}{r - g} \end{align*} \]

这里面有一些参数，决定了DCF的计算过程。

$r$: 折现率
$g$: 永续增长率
$TV$: 终值
$CF_t$: 第t年的现金流(cash flow)
$n$: DCF计算的n年时间

这个公式很简洁，但是问题在于我们该如何理解这个公式呢？本篇文章会讨论我们如何理解这个公式，为什么这个公式是这样计算的，以及如何通过DCF进行评估。

如何理解DCF¶

我认为，理解DCF，必须要理解如下事情：

未来的现金流为什么需要折现?
估值为什么包含未来的现金流？
采取什么样的方式进行折现？
终值 $TV$ 和自然增长率 $g$ 如何计算？

为什么需要折现¶

这个问题很简单，因为未来的钱没有现在的钱值钱，最明显的就是金钱的时间价值。对于现在的钱，我可以立刻用于投资，可以免于通货膨胀或者遭受不确定性。在这个问题上，我没有什么特别大的疑虑，所以不加以阐述。

估值为什么包含未来的现金流¶

为什么给公司定价可以考虑未来一年的现金流¶

DCF讨论的就是未来的现金流如何在现在评估，问出这个问题似乎有些反常，或者说这似乎是一个颠扑不破的常识，但我在学习时，还是在这里迷惑了，为什么估值要考虑未来的现金流呢？

经过一番思考, ...

公司是一种资产，而且可以持续产生现金流（赚钱）。这里为了理解方便，我们假设 股票完全充分的代表公司的价值，并且这里不讨论股价是否被高估或是低估，尽管现实中我们甚至不能够知道公司真正的价值是多少。同样，我们假设公司在盈利/亏损后不进行分红，而是拥有所有的现金流。所以说我们可以得出股票价格($price$), 流通股数($shares$)和公司价值($a$)就满足恒等式：

\[ a = price * shares \]

假设公司第0年股票价格为 $price_0$, 公司A价值 $a_0$。一年过去了，到了第一年，公司A经营了一年，产生了新的现金流，记为 $CF_1$，那么公司的价值成 $a_1 = a_0 +CF_1$ （需要强调的是这是一个极其简单的模型，我们忽略了很多至关重要影响公司价值的因素，但这种假设在理解当前问题上是有价值的）。对于代表拥有公司所有权的股票持有者，公司价值变动将会反映在股票价格上，因为恒等式 $a = price * shares$ 始终成立。

现在我们站在第0年起始的位置来看，如果我们可以肯定公司A可以完成预期增长，增加现金流 $CF_1$，公司会在第一年价值变为 $a_1$, 那么问题就变成了：如果我在第0年的市场上想要购买公司A的股票，多少钱是均衡价格？

这里就带来了一个问题，前面说到我们可以肯定公司A完成预期增长，但你凭什么肯定呢？这就是风险，风险是用来衡量偏离预期的指标，这里需要注意并不一定是向下偏移，超过预期向上偏移同样是风险。为了思考这个问题，我们需要引入一些新的假设，比如无风险债券，来帮助我们排除风险来理解问题本身。

明年天下掉下来10k块钱¶

理解了无风险债券,我们接下来假设如果明年你可以确定天上会掉下来10k块钱, 那么对你来说, 这笔钱是否可以折现到现在? 答案是可以的, 这很自然, 因为未来的该事件是确定的, 现金流被产生了, 所以说在考虑当前资产时候, 是可以被考虑到现在的. 而"可以"是由借贷产生的, 如果不允许借贷, 那么未来的收入根本无法对现在产生任何影响.

如果可以确定, 那么未来可以影响现在, 未来获得的资产也将反映在现在的估值上.

无风险债券¶

此处讨论的无风险债券是指在购买债券后，在约定的到期日可以获得全部的本金和利息. 同样我们讨论静态市场, 利率恒定为5%.

假设目前一张债券票面价值为100元, 为期一年,到期后偿还利率和本金..所以在一年后, 它可以产生5的现金流. 那么我们提出了和上面一样的问题, 在现在的市场上, 买到这张债券需要多少钱?

一种错误的解释是: ~~因为债券是无风险资产, 所以说它的价值等于它的面额, 未来产生的现金流不应该影响现在的价值, 所以说价格应该等于票面价值~~.

尽管这种回答看结果是正确的, 但是他并不是一个正确的逻辑链条. 我们在上面提到,只要未来产生了现金流,我就可以折现到现在, 无论什么原因. 所以说尽管债券到期产生的现金流是为了补偿货币的时间价值, 但它仍然是现金流,仍然参与折现.

而折现意味着定价, 会在当前价格上显示. 补偿货币的时间价值是利息存在的原因, 和折现没有因果关系, 所以不存在"~~因为利息的产生是补偿货币的时间价值, 所以利息产生的现金流不参与折现~~".

正确的逻辑链条是,未来产生的现金流永远会反映在现在, 未来的利息收入作为现金流,应该被反映到现在的价格里去. 这里考虑到利率长久不变, 那么意味着未来产生的现金流完全被用于补偿货币的时间价值, 未来的现金流对现实价值产生了影响, 但由于货币时间价值补偿的存在, 两者差值为0, 结果导致债券的市场价格等于票面价格. 在这种情况下, 折现率=利率=5%.

需要强调的是,在现实中一般折现率和利率并不相同, 所以相同票面价值的债券的市场价值同样存在区别. 这点我们会在后面分析SGOV的章节看到.

无风险资产: 比债券更高的收益¶

到这里, 为什么未来获得的收益可以在现在被考虑进来已经明朗了, 简而言之, 未来确定产生的现金流可以影响现在, 例如通过借贷将未来的钱作用于现在.

考察完债券, 我们这时引入另外一种无风险产品, 记作 ${RFA}$(Risk free asset), 相比于债券他的利率是10%, 同样在一年后偿还本金和利息, 市场利率恒定为5%. 假设该资产的票面价值为100, 我们依然考察 ${RFA}$的市场价格应该是多少?

显然 ${RFA}$的价格不再是票面价值100, 但是为什么呢? 一种错误的思路是, ~~收益超过了对于货币时间价值的补偿~~, 这种思路同样偏离了主线, 因为他试图去研究现金流为什么产生,而不研究为什么未来的现金流可以影响现在.

同样的, 我们可以采取相同的思路,将未来一年产生的现金流折现到现在, 未来一年10k的收益, 折现到现在就是 $ \frac{CF}{1 + r}$. 折现率如何计算呢, 我们这里不讨论, 但总而言之, 本章节已经说明了为什么未来产生的现金流可以被折现到现在. 我们关注为什么"可以", 而不是为什么需要折现.

回到公司本身¶

我们通过无风险资产的例子论证了为什么未来确定的现金流"可以"在考虑现在时包含, 接下来我们回归主题, 探讨为什么这条规则仍然适用于具有风险的公司? 公司的价值不仅仅是目前公司拥有的有形资产，更重要的是其未来持续产生现金流的能力。所以说股票不仅代表了公司的所有权, 也隐含的包括了对未来现金流能力的所有权。

那么，购买的股票（代表公司）就可以产生未来的现金流。即便产生现金流的多少是不确定的，但我们仍然需要将这些不确定的未来现金流反映到当前的估值中。这里，我们不是把问题分开并单独衡量风险和现金流的能力，而是通过调整折现率来量化并应对风险。这很合理，因为未来越不确定，未来产生的现金流对于现在的意义就越小，直觉上我们应该给他一个较低的权重。

在估值过程中，我们将未来带有风险的现金流视为一个“期望值”，这个期望值是在考虑了所有可能性和其概率后得出的一个平均预期。然后，为了补偿投资者承担的风险，我们会使用一个更高的折现率（包含风险溢价）来对这个期望现金流进行折现。因此，尽管我们无法消除风险的存在，但通过在折现率中反映风险，使得“将未来现金流折现到现在”的思路对于公司而言依然有效。

可以折现的一些限制¶

目前将公司未来的现金流折现在现在是正确的，但我们需要考虑我们依然依赖了很多重要的前提条件，如果这些条件失效，那么我们基本不可能对未来产生的现金流折现。比如“可以折现”高度依赖政权稳定、良好的信用体系以及健全的营商环境和法律制定与执行。否则的话，重要的借贷手段实现未来现金流影响现在的手段就会扭曲和失效，我们也自然不能依赖折现的思路了。

这也就意味着，我们需要挑选一个健全、法治、政府稳定的资本市场进行投资，才能使DCF等估值方法具备其应用的基础。

采取怎样的方式进行折现¶

给定一个折现率 $r$, 很自然我们可以得出从现在直到永远现金流的折现金额通过如下公式 $(1)$计算.

公式 $(1)$很简洁，但是问题是使用DCF的时候我们需要估算未来，而离未来越远越不可能准确估计，所以说我们这个从现在算到未来的公式没有什么实践上的意义，我们需要化简它，让他在现实中是可以使用计算的。最终，我们通过引入终值 $TV$(terminate value)来让这个公式更好计算，也即公式$(2)$.

\[ \begin{align*} & DCF = \sum_{t=1}^\infty \frac{CF_t}{(1 + r)^t} &(1) \\\ & DCF = \sum_{t=1}^{n} \frac{CF_t}{(1 + r)^t} + \frac{TV}{(1 + r)^n} &(2) \end{align*} \]

公式 $(1)$和 $(2)$等价，那么我们很自然的可以想出 $\frac{TV}{(1 + r)^n}$ 是一个收敛的值，那么TV如何计算出来呢?

我们需要引入一个自然增长率 $g$, 也即在预测期n之后，现金流在 $[n+1, \infty)$ 区间内以g增长，那么则有关系${CF}_{n+1} = {CF_n} \cdot (1 + g)$.

\[ \begin{align*} DCF &= \sum_{t=n+1}^\infty \frac{CF_t}{(1 + r)^t} \\ &= \sum_{t=n+1}^\infty \frac{CF_{n+1} \cdot (1 + g)^{t-(n+1)}}{(1 + r)^t} \\ &= \frac{CF_{n+1}}{(1 + r)^n} \cdot \sum_{t=1}^\infty \left(\frac{1 + g}{1 + r}\right)^t \end{align*} \]

然后，我们惊奇的发现这里出现了个等比数列的无穷级数, 满足 $S=a+ar+ar^2 +ar^3 + \ldots$

\[ a = \frac{CF_1}{1 + r} \\ r = \frac{1 + g}{1 + r} \]

当 $r < 1$, 即 $\frac{1 + g}{1 + r} < 1$ => $g < r$时，最终的值收敛，我们可以得出TV。反之，如果 $g > r$时，我们是无法得到收敛结果的。这个结果是符合预期的，公司处于稳定状态情况时，增速应该低于现金时间价值，达到收敛状态计算 $TV$. 在长期（尤其是无限期）内，公司的增长不可能永远超过整个经济体系的折现率 $r$，否则公司会无限扩张，最终占据整个经济体，这在现实中不可能。

这里还有一个隐含的结果，无论选择的时间段是3年5年还是10年，DCF算出的结果应该基本一致。这是因为终值（TV）包含了预测期之后所有无限期的现金流折现值。只要你对终值的假设（包括终值开始的现金流、永续增长率g和折现率r）是合理和一致的，那么不同的预测期（n）仅仅是把无限期的现金流拆分成两部分（预测期内和终值），其总和应该保持不变。

如果算出来不一致，说明你算错了，

如何使用DCF¶

DCF的基本概念很简单，将未来的现金流折现在当前，作为企业价值的一部分。那么具体应用的时候，我们仍然会遇到很多具体的问题：

如何计算折现率 $r$
如何计算永续增长率 $g$
如何估算未来的现金流
如何合理的计算 $TV$

如何计算折现率r?¶

折现率r是衡量未来金钱在现在的价值，那么很自然的我们就想到了通货膨胀率这个概念，如果每年产生一定的通货膨胀，表现上货币就消失了过去的购买力，这也是为什么要折现的核心原因。所以我们注意到折现的概念依赖于通货膨胀，如果没有通货膨胀，或者通货紧缩，折现的计算可能与贬值模式下的计算就不同了，因为可能存在未来的钱比现在的钱更值钱的情况出现。注意上文我们提到，未来的现金流反映在现在可以通过借贷来实现，那么我们需要支付利率作为时间价值的补偿。

那这里有一个问题，从通货膨胀上来看，货币的时间价值按照通货膨胀率衰减，也即我们需要按照通货膨胀率来进行折现。而从折现实现的途径来看，我们需要以债券的利率完成折现。那么在计算折现率的时候，究竟是按照通货膨胀，还是按照利率呢？或者说，我们应该如何正确的计算折现率。

首先，通货膨胀和利率是两个独立的概念，没有彼此间的因果关系，尽管他们紧密相连，在实践中美联储经常通过调整利率来调整通货膨胀。费雪公式给出了通货膨胀和名义利率之间的关系, 其中 $i$为名义利率，$r$ 为实际利率，而 $\pi$ 为通货膨胀率。

\[ i \approx r + \pi \]

无风险资产的折现率：Zero Coupon¶

由于名义利率已经考虑到了通货膨胀，所以对于无风险资产来说，折现率就是名义利率。这个时候，我们可以关注一种零风险债券，zero coupon bond. 这种债券通常为长期债券，它在到期前不支付任何利息（票息），所有的收益都体现在买入时的折价和到期时获得的面值之间的差额。零息债券完美符合了我们在学习DCF时候的场景，也即在未来产生现金流，如何折现到现在，这有一个成熟的公式：

\[ PV = \frac{FV}{(1+r)^N} \]

$PV$是现价， $TV$是终值， $r$是市场上的零息利率， $N$是距离债券到期的时间。

这里我们看到了熟悉的折现公式，这很合理，但需要注意的是我们的折现率采取的是现在的市场利率，你可以在美国财政部官网找到这些目前的数据。这就产生了一个问题，尽管债券是无风险资产，但未来的利率不确定，为什么我们在计算折现的时候仍然使用当前的利率呢？

换句话说，当前公式假设了N年直到到期，市场汇率维持不变始终为r，那么这其实是一个和现实不符的重要假设，那为什么这个公式还准确呢？同样的，DCF在计算折现率的时候也采用了这个假设。

这个问题的回答在于我们如何理解利率 $r$, 上面假设了一个静态的利率，但实践中这个利率是市场均衡的结果，代表了对未来债券收益的共识，这个回报率已经考虑了市场对未来短期利率走势（是会上升还是下降）、通胀预期、经济增长前景、以及美联储货币政策等所有信息的共识性预期。

所以说，我们在计算折现的时候，并不是_{~假设了N年直到到期，市场汇率维持不变始终为r}~，这是一个错误的思路，尽管看起来产生了相同的结果。而是认为市场形成的价格充分反映了对未来的预期，是用来衡量资产现在价格的最佳指标，由于我们不可能比市场做得更好，我们找不到比市场数据本身更好反应未来的数据，所以我们使用当前市场达成对未来最佳估计的数据，对未来进行估算。

所以结论是，对于无风险无息债券，折现率等于现在市场的利率，一个已经包含了通货膨胀和对未来预期的价格。

无风险资产的折现率：Coupon Bond¶

Coupon Bond，也即附息债券，在债券的生命周期内，发行人会定期（通常是每年或每半年）向债券持有人支付固定金额的利息。这个金额通常是债券面值（Face Value 或 Par Value）乘以票面利率（Coupon Rate）来计算的。

我们开始分析，具有产生现金流的能力，到期后会偿还票面价值，于是我们写一个折现公式用来表示当前定价，正如下面的公式。乍一看，惊奇的发现，欸这个玩意怎么长得和DCF的样子这么像呢？仔细一看，哦，原来他就是一个DCF公式。再一看产生现金流的能力，欸一模一样！

\[ PV = \sum_{t=1}^{N} \frac{C}{(1+r_t)^t} + \frac{FV}{(1+r_N)^N} \]

那么在我们对现在进行估值的时候，我们可以直接使用市场达成均衡的利率 $r$代入公式。在这个情况下，未来究竟是分红一次，还是分红多次，我们计算的思路都是一样的，无非是附息债券需要求和。

风险资产：风险溢价¶

我们已经搞明白无风险利率的折现计算逻辑了，那么这个时候我们开始考虑风险资产，顾名思义，风险资产相比于债券等无风险资产，包含了风险。太简单了，我一眼就能看出来区别，那在dcf的时候，我们需要为此部分做估值吗，如果需要，如何估值呢？

前一个问题很好回答，我们必须对风险予以补偿，否则任何一个理性人都会选择无风险资产，没有人会选择相同收益的风险资产。当然，有时人并不是理性人，或者人被暴力等原因强迫，这些情况不在我们讨论的情况。

那么，我们如何对风险进行补偿呢？很自然的，我们将风险补偿拆分成两块，一部分是风险，一部分是补偿。对于风险的评估是一回事，而对于风险的补偿是另外一回事。打个很简单的比方，轧路机前面捡任何东西的风险都是相同的，而压路机前捡到的东西（理解为补偿）是不同的，这是两个逻辑上独立的概念，当然，通常我们认为他们有正相关，即风险越高，获得的补偿应该更高。

风险评估与定价¶

ERP¶

股权风险溢价 (Equity Risk Premium, ERP) 是投资者投资股票市场相对于无风险投资（如政府债券）所要求的额外回报。它反映了股票市场整体的风险。

用大白话说，就是我知道投资有风险，于是为了消除行业等非系统性风险，我投资指数，但投资指数并不能消除非系统性风险，所以说ERP其实就代表了**所有投资者**对整个大盘系统性风险的**评估**。

以轧路机为例，ERP的核心是对轧路机风险的评估，因为轧路机的速度等可能会改变，ERP也会改变。理论上，轧路机前的物品价值并不会影响ERP，但是实际上人们可能会因为物品价值而盲目导致ERP的大幅变化。

既然是评估，那么ERP就会动态发生变化，他受事件影响，因为投资者的情绪会受到事件产生的情绪的影响，但长期来看ERP趋于稳定。

beta¶

我们可以通过定量和定性分析一些风险，最经典的就是 $\beta$. $\beta$ 衡量的是当市场收益率变化 1% 时，个股收益率平均变化多少个百分点。他是对于波动率的衡量标准，也就是说它必须有一个基准，这个基准就是ERP。

\[ \begin{equation} \beta_i = \frac{Cov(R_i, R_m)}{Var(R_m)} \end{equation} \]

其中 $R_i$ 代表资产 $i$ 的收益率， $R_m$ 代表市场组合的收益率， $Cov$ 表示协方差， $Var$ 表示方差。

我们可以注意到 $\beta$ 是过去每一刻市场对于风险的反应，这里引用经典的一句话“过往业绩不代表未来”，但问题是市场对风险的评估总比一个人准确，我们找不到更好的风险评估数据来对个股未来相对于市场收益变化比例的数据。所以说，对于$\beta$的使用，我们通常使用最新的数据作为对未来的预估，以及作为对过去市场投资者对这只个股的整体看法。

轧路机为例，$\beta$就是轧路机前物品相对移动的情况，如果物品不动，那么 $\beta = 1$, 如果物品朝着远离轧路机的方向运动，$\beta < 1$. 需要强调的是，beta在这个例子中和物品的价值无关，因为beta描述的是对于标准风险的偏移，只和相对轧路机移动的快慢有关。

资本资产定价模型 (CAPM)¶

股权成本 $K_e$ 解决了如何为风险资产定价的问题。ERP和beta构成了风险资产评估的部分，他衡量了投资者如何理解当前风险资产，我们可以通过此指标来计算出投资者期望的收益。债券投资者期望的收益就是当前的利率，但对于风险资产来说，除了无风险利率之外，投资者希望得到额外的补偿，对风险的补偿就是 $\beta * ERP$、这里的风险补偿对于投资者来说，代表了只有产生了额外收益用来补偿持有股权产生的风险，才会持有这家公司的股票。所以说，对于投资者来说，他对持股产生的收益预期就是$K_e$:

\[ K_e = R + \beta * ERP \]

投资者期望持有股权的收益是 $K_e$, 这也是投资者从这笔股权投资中获得的最低预期回报率。如果实际收益低于 $K_e$, 那么理性的投资者就不会投资。

这里我们通过系统的策略对风险定价，将风险转换成可量化的预期回报要求，在后续的估值或投资决策计算中，我们就可以在一个“风险调整后”的框架下进行操作，这使得计算过程在形式上可以类比于处理无风险资产，因为风险的补偿已经内生于我们所使用的折现率或要求回报率中。尽管存在unknown unknowns类的风险，但我们认为ERP已经对这部分进行了定价，尽管并不充分，因为没有人知道未来会发生什么，但ERP是有效市场能够达成最佳的评估。

风险资产成本与折现率¶

资本资产定价模型描述了投资者在承担风险后，最低能够接受的收益率，这也就是企业的融资成本。比如$K_e$是6%时，企业每融资100块，他必须给予他的股权持有人6块的回报才能够满足这些投资者，如果他不能够满足这个最低要求，投资者就可能会撤资。

但对于DCF，我们关注折现率，折现率和风险资产成本有什么关系呢？事实上，折现率等于风险资产成本。让我们先忽略“风险”这个特征而只关注成本，这样做是合理的，正如前文指出，通过系统的对风险定价，计算形式上会类似于无风险资产。股权成本也是成本，类似于债券，对于企业来说，可以通过提供股权的手段在当前获得未来的钱，正如债券通过借贷手段在当前获取未来的钱一样。那么自然而然的我们就可以意识到，折现率就等于成本。所以说对于风险资本，尽管资产蕴含风险，但通过对风险定价，我们就可以得到折现率。

WACC(Weighted Average Cost of Capital)¶

上文讲的 $K_e$说明了股权持有成本，但他没有考虑企业的负债情况，对于企业存在不可忽略的负债，而且考虑负债时候，不能很好展示资产成本，所以我们引入了wacc这个概念，充分了考虑负债产生的影响。

\[ \text{WACC} = \frac{E}{E + D} \cdot r_e + \frac{D}{E + D} \cdot r_d \cdot (1 - T) \]

其中：

$E$ : 股权的市场价值（Equity）
$D$: 债务的市场价值（Debt）
$r_e$: 股权成本率（Cost of Equity）
$r_d$: 债务成本率（Cost of Debt）
$T$: 企业的税率（Tax Rate）

请注意，这里的 $r_e$就是上面所说的 $K_e$, 不过$K_e$更常见于理论模型，如 CAPM； $r_e$更常见于实际应用场景，如 WACC 计算。

在计算出wacc之后，我们就可以使用这个作为折现率来计算DCF指标了。

估算增长率，计算现金流¶

首先我们需要估计未来若干段时间的增长率，然后我们就可以计算出未来各个年度增长的收益。由于增长率**不等于**产生现金流，我们仍然需要结合各种因素来从增长率得到具体产生现金流的数量。增长率通常来讲说的是经营收入Revenue上的增长, 经营收入也正是企业产生现金流的体现。Revenue抵达现金流的过程需要扣除一些开销，这很正常，企业的运行需要花销。通常来讲，我们把开销分为COGS(Cost of Good Sells), 也即直接和售出物品相关的费用，其次是Operation Cost, 指的是和销售产品无直接关系的费用，例如SG&A(Selling, General, and Administrative expenses)所指的行政费用，和R&D研发费用。因为最终产生的现金流需要扣除各部分，于是通常可以用桑基图（Sankey Diagram），用于直观地展示数据的流动和分布，比如alphaspread提供的Google Revenue & Expenses Breakdown的图:

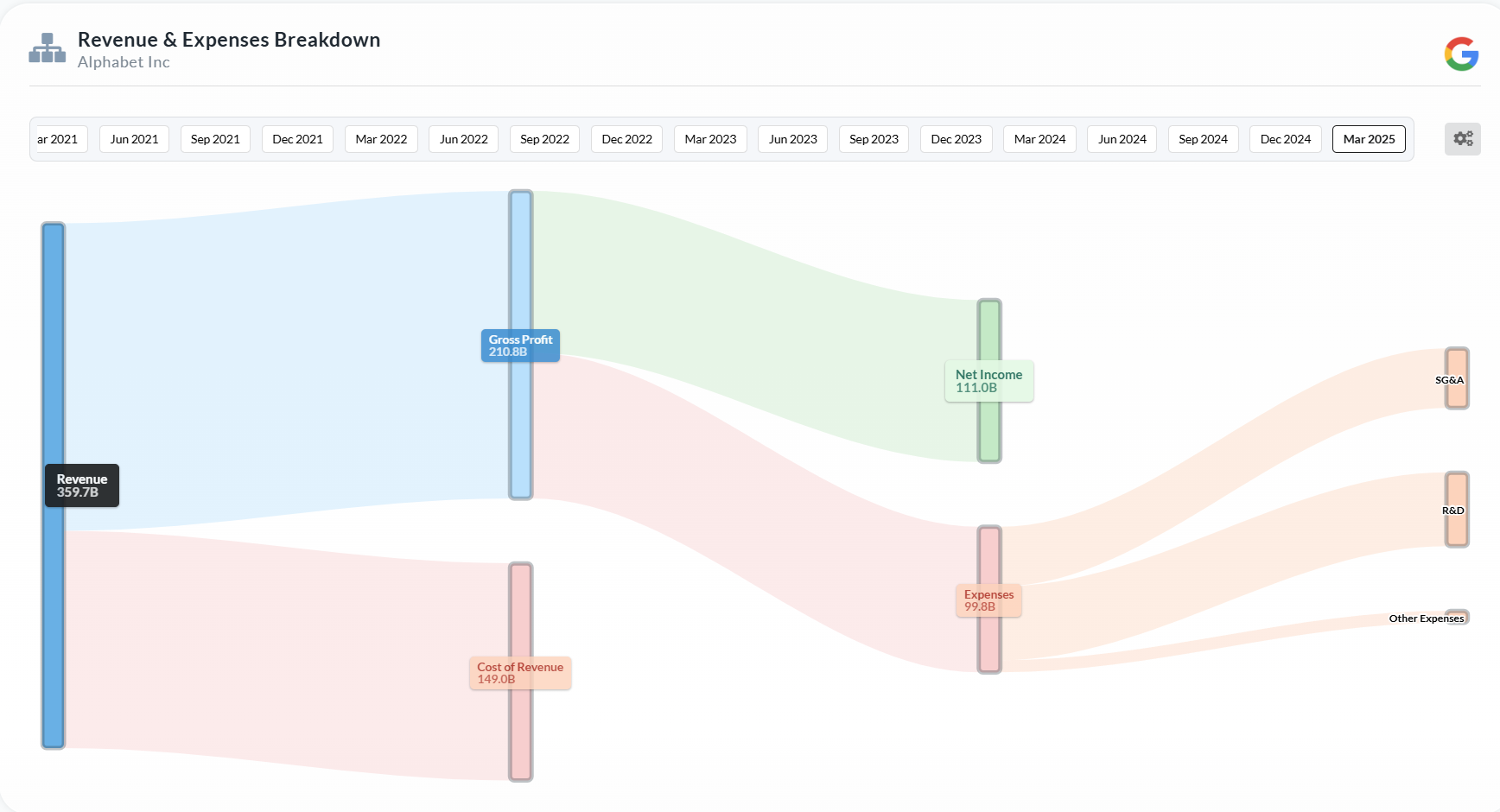
google revenue & expenses breakdown

这个图清晰地展示了我们如何从Revenue到达net income，也即获取到的净收入。需要强调是，这里net income和Free cash flow仍有一定区别，因为net income是采取权责发生制的会计手段，核心是“收入与费用在发生时确认”，而不是在现金实际流入或流出时确认。例如，营收为 10 million，但其中有 2 million 是应收账款。尽管现金尚未实际流入，但在权责发生制下，Revenue 仍然会被记录为 10 million。这也解释了为什么权责发生制的净利润（Net Income）不能直接反映实际的现金流情况。

这里引入了EBIT(Earnings Before Interest and Taxes)的概念，也即 $ EBIT = Revenue - COGS - Operation Cost$.

而使用DCF，显然我们不能关注net income这个权责发生制下的净利润，而应该关注现金流。那么自然，所有的开销我们都开始关注流入流出的现金流，虽然 COGS 和 Operation Costs 的总金额可能与权责发生制下相同，但它们在现金流中的记录时间可能不同。例如，企业可能会提前支付供应商款项或推迟支付账单，这会导致现金流和权责发生制下的费用确认产生时间差。

除此之外，我们需要关注额外一些不同于权责发生制的内容，第一是资本支出CapEx，资本支出当然不影响净利润，因为它被认为是投资活动的一部分，而不是经营活动的一部分。CapEx 会通过折旧的方式，逐步影响净利润。但在现金流的计算中，CapEx 是一次性扣减的（作为现金流出）。第二就是折旧费用和摊销，现金流模式下的会计准则下这部分内容并不真正消耗现金流，需要在计算FCF时加回去。

那么我们就可以通过以下自由现金流DCFF的计算公式来计算当年产生的自由现金流：

\[ \text{FCFF} = \text{EBIT} \times (1 - T) + \text{D\&A} - \Delta \text{WC} - \text{CapEx} \]

EBIT × (1 - T): 税后息税前利润，表示企业在扣除税费后的经营收益。
D&A: 折旧与摊销，是非现金费用，需要加回。
ΔWC: 营运资本变化，反映了经营活动中流动资产和流动负债的变化。
CapEx: 资本支出，企业用于购买固定资产或长期资产的支出，从现金流中扣除。

需要指出的是，我们在估算现金流时，并不总是采取这个公式，比如对一个公开交易的大型公司，其历史自由现金流数据通常是直接可查的。通过分析其FCF占收入的比例（即FCF利润率），可以快速且相对准确地捕捉公司将收入转化为现金流的效率。这简化了预测过程，避免了对EBIT、折旧与摊销（D&A）、营运资本变动（ΔWC）和资本支出（CapEx）等多个变量进行独立预测的复杂性。我们可以直接采取了稳定性假设，通过容易获得的数据和适度简化，我们可以快速获取到关键数据，强调关键驱动因素。

但这个公式本身可以被更广泛的应用，进行敏感性分析和情景分析。

如何使用DCF指标¶

在了解了DCF的核心思路和各个指标之后，可以做一些实践应用DCF公式。需要注意的是，由于预测现金流对于仍然发生亏损的公司较为困难，可以找首先比较稳定的公司进行实践，之后再慢慢学习如何对仍然发生亏损的公司进行评估。

本章节的很多内容是Gemini提供的，赞美它教我知识带我练习。

数据收集与准备¶

在计算 $K_e$时候，我们需要R, $/beta$ 和 $ERP$, 由于这些数据基本都是宏观层面的数据，所以我们并不需要自己计算。当然，即便自己计算，自己是否计算的比别人的好，是有疑问的。所以可以直接采取现成的数据。对于$ERP$来说，由于他是一个对市场的评估，所以不同机构会得出自己的结果，例如金融平台，估值机构，审计机构和投资银行。而beta由于计算公式相对固定，加上数据更易得到，影响因数较少，较容易得出。

这里练习目的，可以暂时使用Alpha Spread 提供的数据。

Google¶

1. 寻找市场数据¶

选择Google的原因是我买过Google的票，以及Google仍然在增长并且相对稳定，我认为很适合DCF的使用场景。根据alphaspread提供的数据:

R	$\beta$	ERP
4.35%	0.83	4.12%

平台同样提供好了根据上述值计算的 $K_e$，和历史波动值。同样的，平台也计算好了wacc, 当前结果为：

$K_e$	wacc
7.76%	7.75%

2. 预测未来增长率¶

在获取到wacc之后，我们需要关注历史增长率来**预测未来增长率**，尽管过去的数据无法预测未来，但我们仍然相信当前的数据能够更好的代表现状，来预测未来。

2022年：9.78% = 2023年：8.68%
2024年：13.87% 参考 Google 历史表现显示的过去几年增长率在 8%-14% 之间）以及对其未来增长的共识预测。于是我们对增长率做出以下评估：
2025: 12%
2026: 10%
2027: 8%

3. 自由现金流利润率¶

随后，我们关注自由现金流利润率 (FCF Margin)

= 2024年 FCF Margin: 72.764B / 350.018B (2024年收入) ≈ 20.79% - 2023年 FCF Margin: 69.495B / 307.394B (2023年收入) ≈ 22.61% - 2022年 FCF Margin: 60.010B / 282.836B (2022年收入) ≈ 21.22%

所以我们假定未来三年FCF利润率稳定在 21.5%，

4. 计算未来收入和现金流¶

2024年收入 (参考基准)： 350.018B (数据来源：Macrotrends)
2025年收入： 350.018B * (1 + 12%) = 392.020B
2026年收入： 392.020B * (1 + 10%) = 431.222B
2027年收入： 431.222B * (1 + 8%) = 465.719B

5. 计算自由现金流现值¶

2025年 FCF 现值： 84.284B / (1 + 0.0775)^1 = 84.284B / 1.0775 ≈ 78.225B
2026年 FCF 现值： 92.713B / (1 + 0.0775)^2 = 92.713B / 1.1610 ≈ 79.856B
2027年 FCF 现值： 100.039B / (1 + 0.0775)^3 = 00.039B / 1.2511 ≈ 79.959B

6. 计算终值¶

\[ TV = 100.039B * (1 + 0.03) / (0.0775 - 0.03) = 2169.263B \]

7. 企业价值和股权价值¶

终值的现值 = $ \frac{2169.263B}{ (1+0.0775)^3 } = 2169.263B / 1.2511 \approx 1733.864B $
企业价值 = 238.040B + 1733.864B = 1971.904B

数据来源： Alphabet 2024年报显示，截至2024年底，总现金、现金等价物和有价证券约为 110.916B，长期债务约为 11.870B。

股权价值 = 1971.904B + 99.046B = 2070.950B
每股估值 = 2070.950B / 13.313B 股 ≈ 155.56 / 股

这里我们可以看到如果我们假设google只增长三年，随后进入稳定状态，他的股票价格实际上是远低于当前股价的。这就说明事实上我们预计google仍将在未来持续增长，在这种情况下，我们将延长增长的预估时间，比如我们预估google将在未来十年持续增长。需要强调的是我们绝不能通过调整终值永续增长率来调整我们的结果。